Az óra céljai:
Általános oktatás:
- ellenőrizze a tanulók elméleti ismereteit (a derékszögű háromszög tulajdonságait, a Pitagorasz-tételt), azok felhasználási képességét a feladatok megoldásában;
- problémahelyzetet teremtve vezesse el a tanulókat az inverz Pitagorasz-tétel „felfedezéséhez”.
fejlesztés:
- az elméleti ismeretek gyakorlati alkalmazásához szükséges készségek fejlesztése;
- a következtetések megfogalmazásának képességének fejlesztése a megfigyelések során;
- memória, figyelem, megfigyelés fejlesztése:
- tanulási motiváció fejlesztése a felfedezésekből származó érzelmi elégedettséggel, a matematikai fogalmak fejlődéstörténeti elemeinek bemutatásával.
nevelési:
- állandó érdeklődés ápolása a téma iránt Pythagoras életének tanulmányozása révén;
- a kölcsönös segítségnyújtás és az osztálytársak tudásának objektív értékelése szakértői értékelésen keresztül.
Óraforma: óra-óra.
Tanterv:
- Idő szervezése.
- Házi feladat ellenőrzése. Tudásfrissítés.
- Gyakorlati feladatok megoldása a Pitagorasz-tétel segítségével.
- Új téma.
- A tudás elsődleges megszilárdítása.
- Házi feladat.
- Az óra eredményei.
- Önálló munka (egyéni kártyák szerint Pythagoras aforizmáinak kitalálásával).
Az órák alatt.
Idő szervezése.
Házi feladat ellenőrzése. Tudásfrissítés.
Tanár: Milyen feladatot végeztél otthon?
Diákok: Adott egy derékszögű háromszög két oldala, keresse meg a harmadik oldalt, és rendezze a válaszokat táblázatba. Ismételje meg a rombusz és egy téglalap tulajdonságait. Ismételjük meg, amit feltételnek neveznek, és mi a tétel következtetése. Készítsen jelentéseket Pythagoras életéről és munkásságáról. Hozz magaddal egy 12 csomós kötelet.
Tanár: Ellenőrizze a házi feladatokra adott válaszokat a táblázat alapján!
(az adatok feketével, a válaszok pirossal).
Tanár: A nyilatkozatok fel vannak írva a táblára. Ha egyetért velük, a megfelelő kérdésszámmal szemben lévő papírlapokon tegye a „+”, ha nem ért egyet, akkor „-” jelet.
A nyilatkozatok fel vannak írva a táblára.
- A hypotenus nagyobb, mint a láb.
- Egy derékszögű háromszög hegyesszögeinek összege 180 0 .
- Egy derékszögű háromszög területe lábakkal aés ban ben képlettel számítjuk ki S=ab/2.
- A Pitagorasz-tétel minden egyenlő szárú háromszögre igaz.
- Egy derékszögű háromszögben a 30 0 szöggel szemközti láb egyenlő a befogó felével.
- A lábak négyzeteinek összege megegyezik a hipotenusz négyzetével.
- A láb négyzete egyenlő a hipotenusz és a második láb négyzeteinek különbségével.
- Egy háromszög oldala egyenlő a másik két oldal összegével.
A munkákat szakértői értékeléssel ellenőrzik. Az ellentmondásos kijelentéseket megvitatják.
Kulcs az elméleti kérdésekhez.
A tanulók a következő rendszer szerint értékelik egymást:
8 helyes válasz „5”;
6-7 helyes válasz „4”;
4-5 helyes válasz „3”;
kevesebb, mint 4 helyes válasz „2”.
Tanár: Miről beszéltünk az utolsó órán?
Diák: Pythagorasról és tételéről.
Tanár: Fogalmazza meg a Pitagorasz-tételt! (Több tanuló elolvassa a fogalmazást, ilyenkor 2-3 tanuló bizonyít a táblánál, 6 tanuló az első asztaloknál a lapokon).
A kártyákon lévő mágnestáblára matematikai képletek vannak felírva. Válassza ki azokat, amelyek tükrözik a Pitagorasz-tétel jelentését, ahol a és ban ben - katéterek, Val vel - hypotenus.
| 1) c 2 \u003d a 2 + b 2 | 2) c \u003d a + b | 3) a 2 = 2-től 2-ig |
| 4) c 2 \u003d a 2 - a 2-ben | 5) 2-ben \u003d c 2 - a 2 | 6) a 2 \u003d c 2 + a 2-ben |
Míg a táblánál és a terepen a tételt bizonyító hallgatók nem állnak készen, a szót azok kapják, akik Pitagorasz életéről és munkásságáról készítettek jelentéseket.
A terepen dolgozó iskolások szórólapokat adnak át, és meghallgatják a táblánál dolgozók tanúit.
Gyakorlati feladatok megoldása a Pitagorasz-tétel segítségével.
Tanár: Gyakorlati feladatokat ajánlok a tanult tétel felhasználásával. Először az erdőt látogatjuk meg, vihar után, majd vidéken.
1. feladat. A vihar után letört a luc. A fennmaradó rész magassága 4,2 m. Az alaptól a ledőlt csúcsig a távolság 5,6 m Keresse meg a lucfenyő vihar előtti magasságát!
2. feladat. A ház magassága 4,4 m A ház körüli pázsit szélessége 1,4 m Milyen hosszúra kell elkészíteni a létrát, hogy ne lépjen a gyepre és elérje a ház tetejét?
Új téma.
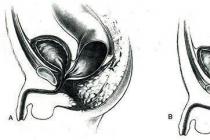
Tanár:(zene szól) Csukd be a szemed, néhány percre belemerülünk a történelembe. Veled vagyunk az ókori Egyiptomban. Itt a hajógyárakban építik az egyiptomiak híres hajóikat. De a földmérők, olyan telkeket mérnek, amelyeknek a határait a Nílus áradása után elmosta. Az építők grandiózus piramisokat építenek, amelyek még mindig lenyűgöznek bennünket a nagyszerűségükkel. Mindezen tevékenységek során az egyiptomiaknak derékszöget kellett használniuk. Tudták, hogyan kell megépíteni őket egy 12 csomós kötél segítségével, amelyek egymástól azonos távolságra voltak megkötve. Próbáld meg, és te, úgy vitatkozva, mint az ókori egyiptomiak, építs derékszögű háromszögeket a köteleid segítségével. (Ezt a feladatot megoldva a srácok 4 fős csoportokban dolgoznak. Egy idő után valaki a táblánál egy háromszög felépítését mutatja a táblagépen).
A kapott háromszög oldalai 3, 4 és 5. Ha ezek közé a csomók közé még egy csomót kötünk, akkor az oldalai 6, 8 és 10 lesznek. Ha kettő - 9, 12 és 15. Ezek a háromszögek téglalap alakúak, mert .
5 2 \u003d 3 2 + 4 2, 10 2 \u003d 6 2 + 8 2, 15 2 \u003d 9 2 + 12 2 stb.
Milyen tulajdonságokkal kell rendelkeznie egy háromszögnek, hogy derékszögű legyen? (A tanulók maguk próbálják megfogalmazni az inverz Pitagorasz-tételt, végül valakinek sikerül).
Miben különbözik ez a tétel a Pitagorasz-tételtől?
Diák: A feltétel és a következtetés felcserélődik.
Tanár: Otthon megismételted, hogy hívják az ilyen tételeket. Akkor most mire készülünk?
Diák: Az inverz Pitagorasz-tétellel.
Tanár: Írd le a füzetedbe az óra témáját. Nyissa ki a 127. oldalon található tankönyveit, olvassa el még egyszer ezt az állítást, írja le a füzetébe, és elemezze a bizonyítást.
(Több perces önálló munka után a tankönyvvel, ha kívánja, egy személy a táblánál bizonyítja a tételt).
- Mi a neve egy háromszögnek, amelynek 3, 4 és 5 oldala van? Miért?
- Milyen háromszögeket nevezünk Pitagorasz-háromszögeknek?
- Milyen háromszögekkel dolgoztál a házi feladatodban? És a fenyőfával és a létrával kapcsolatos problémákban?
A tudás elsődleges megszilárdítása
.Ez a tétel segít megoldani azokat a problémákat, amelyekben meg kell találni, hogy a háromszögek derékszögű háromszögek-e.
Feladatok:
1) Állapítsa meg, hogy egy háromszög derékszögű-e, ha az oldalai egyenlőek:
a) 12,37 és 35; b) 21., 29. és 24.
2) Számítsa ki egy 6, 8 és 10 cm oldalú háromszög magasságát!
Házi feladat
.127. oldal: Inverz Pitagorasz-tétel. 498. sz. (a, b, c) 497. sz.
Az óra eredményei.
Milyen újdonságokat tanultál a leckében?Önálló munkavégzés (egyedi kártyákon végezve).
Tanár: Otthon megismételted a rombusz és a téglalap tulajdonságait. Sorolja fel őket (beszélgetés van az osztállyal). Az utolsó leckében arról beszéltünk, hogy Pythagoras sokoldalú ember volt. Orvostudományokkal, zenével és csillagászattal foglalkozott, emellett sportoló volt és részt vett az olimpiai játékokon. Pythagoras filozófus is volt. Számos aforizmája még ma is aktuális számunkra. Most a saját munkáját fogja végezni. Minden feladathoz több válasz is szerepel, melyek mellé pitagoraszai aforizmák töredékeit írják. Az Ön feladata az összes feladat megoldása, a kapott töredékekből kimutatás és lejegyzés.
A Pitagorasz-tétel ezt mondja:
Egy derékszögű háromszögben a lábak négyzeteinek összege egyenlő a befogó négyzetével:
a 2 + b 2 = c 2,
- aés b- derékszöget képező lábak.
- Val vel a háromszög befogója.
A Pitagorasz-tétel képletei
- a = \sqrt(c^(2) - b^(2))
- b = \sqrt (c^(2) - a^(2))
- c = \sqrt (a^(2) + b^(2))
A Pitagorasz-tétel bizonyítása
A derékszögű háromszög területét a következő képlettel számítjuk ki:
S = \frac(1)(2)ab
Egy tetszőleges háromszög területének kiszámításához a képlet a következő:
- p- félperiméter. p=\frac(1)(2)(a+b+c) ,
- r a beírt kör sugara. Egy téglalaphoz r=\frac(1)(2)(a+b-c).
Ezután egyenlővé tesszük mindkét képlet jobb oldalát egy háromszög területére:
\frac(1)(2) ab = \frac(1)(2)(a+b+c) \frac(1)(2)(a+b-c)
2 ab = (a+b+c) (a+b-c)
2 ab = \left((a+b)^(2) -c^(2) \jobb)
2ab = a^(2)+2ab+b^(2)-c^(2)
0=a^(2)+b^(2)-c^(2)
c^(2) = a^(2)+b^(2)
Inverz Pitagorasz-tétel:
Ha egy háromszög egyik oldalának négyzete egyenlő a másik két oldal négyzeteinek összegével, akkor a háromszög derékszögű háromszög. Vagyis a pozitív számok tetszőleges hármasára a, bés c, oly módon, hogy
a 2 + b 2 = c 2,
van egy derékszögű háromszög lábakkal aés bés hypotenusa c.
Pitagorasz tétel- az euklideszi geometria egyik alaptétele, amely a derékszögű háromszög oldalai közötti kapcsolatot megállapítja. Püthagorasz, a tudós matematikus és filozófus bebizonyította.
A tétel jelentése abban, hogy más tételek bizonyítására és problémák megoldására használható.
Kiegészítő anyag:
Az iskolai tanterv témáinak figyelembevétele videoleckék segítségével kényelmes módja az anyag tanulmányozásának és asszimilálásának. A videó segít a hallgatók figyelmét a fő elméleti pontokra összpontosítani, és nem hagyja figyelmen kívül a fontos részleteket. Ha szükséges, a tanulók bármikor újra meghallgathatják a videóleckét, vagy visszatérhetnek néhány témához.
Ez a 8. osztályos oktatóvideó segít a tanulóknak új geometriai téma elsajátításában.
Az előző témakörben a Pitagorasz-tételt tanulmányoztuk és elemeztük annak bizonyítását.
Van egy tétel is, amelyet inverz Pitagorasz-tételként ismernek. Tekintsük részletesebben.
Tétel. Egy háromszög derékszögű, ha teljesíti az egyenlőséget: a háromszög egyik oldalának négyzetes értéke megegyezik a másik két oldal négyzetének összegével.

Bizonyíték. Tegyük fel, hogy kapunk egy ABC háromszöget, amelyben igaz az AB 2 = CA 2 + CB 2 egyenlőség. Be kell bizonyítanunk, hogy a C szög 90 fok. Tekintsünk egy A 1 B 1 C 1 háromszöget, amelyben a C 1 szöge 90 fok, a C 1 A 1 oldal egyenlő a CA-val és a B 1 C 1 oldal egyenlő a BC-vel.
A Pitagorasz-tételt alkalmazva felírjuk az A 1 C 1 B 1 háromszög oldalainak arányát: A 1 B 1 2 = C 1 A 1 2 + C 1 B 1 2. A kifejezést egyenlő oldalakra cserélve A 1 B 1 2 = CA 2 + CB 2 -t kapunk.
A tétel feltételeiből tudjuk, hogy AB 2 = CA 2 + CB 2 . Ekkor felírhatjuk, hogy A 1 B 1 2 = AB 2, amiből következik, hogy A 1 B 1 = AB.
Azt találtuk, hogy az ABC és A 1 B 1 C 1 háromszögek három oldala egyenlő: A 1 C 1 = AC, B 1 C 1 = BC, A 1 B 1 = AB. Tehát ezek a háromszögek egybevágóak. A háromszögek egyenlőségéből az következik, hogy a C szög egyenlő a C 1 szöggel, és ennek megfelelően egyenlő 90 fokkal. Megállapítottuk, hogy az ABC háromszög derékszögű háromszög, és C szöge 90 fok. Ezt a tételt bebizonyítottuk.

Ezután a szerző egy példát mond. Tegyük fel, hogy kapunk egy tetszőleges háromszöget. Oldalainak méretei ismertek: 5, 4 és 3 egység. Ellenőrizzük az állítást a Pitagorasz-tételre fordított tételből: 5 2 = 3 2 + 4 2 . Ha az állítás helyes, akkor az adott háromszög derékszögű háromszög.
A következő példákban a háromszögek is derékszögűek lesznek, ha az oldaluk egyenlő:
5, 12, 13 egység; a 13 2 = 5 2 + 12 2 egyenlőség igaz;
8, 15, 17 egység; a 17 2 = 8 2 + 15 2 egyenlet igaz;
7, 24, 25 egység; a 25 2 = 7 2 + 24 2 egyenlet igaz.
A Pitagorasz-háromszög fogalma ismert. Ez egy derékszögű háromszög, amelynek oldalértékei egész számok. Ha a Pitagorasz-háromszög lábait a és c, valamint a b hipotenusz jelöli, akkor ennek a háromszögnek az oldalai a következő képletekkel írhatók fel:
b \u003d k x (m 2 - n 2)
c \u003d k x (m 2 + n 2)
ahol m, n, k bármely természetes szám, és m értéke nagyobb, mint n.

Érdekes tény: az 5, 4 és 3 oldalú háromszöget egyiptomi háromszögnek is nevezik, ilyen háromszög ismert volt az ókori Egyiptomban.
Ebben a videós oktatóanyagban megismerkedtünk a tétellel, a Pitagorasz-tétel fordítottjával. Fontolja meg részletesen a bizonyítékot. A tanulók azt is megtanulták, hogy mely háromszögeket nevezik Pitagorasz-háromszögeknek.
A tanulók ennek a videós leckének a segítségével önállóan is könnyen megismerkedhetnek a "Tétel, a Pitagorasz-tétel inverze" témával.
Van der Waerden szerint nagyon valószínű, hogy az arány általános formában már ismert volt Babilonban az ie 18. század körül. e.
Körülbelül Kr.e. 400. azaz Proklosz szerint Platón módszert adott a Pitagorasz-hármasok megtalálására, az algebra és a geometria kombinálására. Kr.e. 300 körül e. Eukleidész "Elemeiben" megjelent a Pitagorasz-tétel legrégebbi axiomatikus bizonyítéka.
Megfogalmazás
A fő megfogalmazás algebrai műveleteket tartalmaz - derékszögű háromszögben, amelynek lábainak hossza egyenlő a (\displaystyle a)és b (\displaystyle b), és a hypotenus hossza az c (\displaystyle c), az összefüggés teljesül:
.Egy ekvivalens geometriai megfogalmazás is lehetséges, a terület-ábra fogalmához folyamodva: derékszögű háromszögben a hipotenuzusra épített négyzet területe megegyezik a lábakra épített négyzetek területeinek összegével. Ebben a formában a tétel Euklidész Principiájában van megfogalmazva.
Inverz Pitagorasz-tétel- tetszőleges háromszög derékszögűségére vonatkozó állítás, amelynek oldalainak hosszát a reláció összefügg a 2 + b 2 = c 2 (\displaystyle a^(2)+b^(2)=c^(2)). Következésképpen a pozitív számok bármely hármasára a (\displaystyle a), b (\displaystyle b)és c (\displaystyle c), oly módon, hogy a 2 + b 2 = c 2 (\displaystyle a^(2)+b^(2)=c^(2)), van egy derékszögű háromszög lábakkal a (\displaystyle a)és b (\displaystyle b)és hypotenusa c (\displaystyle c).
Bizonyítéka
A Pitagorasz-tételnek legalább 400 bizonyítását rögzítették a tudományos irodalomban, amit egyrészt a geometria alapvető értékével, másrészt az eredmény elemi jellegével magyaráznak. A bizonyítások fő irányai: az elemek arányának algebrai használata háromszög (ilyen pl. a népszerű hasonlósági módszer), területmódszer, léteznek különféle egzotikus bizonyítások is (például differenciálegyenletek segítségével).
Hasonló háromszögeken keresztül
Euklidesz klasszikus bizonyítása azt a célt szolgálja, hogy megállapítsa a téglalapok közötti területek egyenlőségét a befogó feletti négyzet és a lábak feletti négyzetek derékszögű magasságának felmetszésével.
A bizonyításhoz használt konstrukció a következő: derékszögű derékszögű háromszögre C (\displaystyle C), négyzetek a lábak felett és és négyzetek a hipotenuzus felett A B I K (\displaystyle ABIK) magasság épül CH (\displaystyle CH)és az azt folytató sugár s (\displaystyle s), a befogó feletti négyzetet két téglalapra osztva és . A bizonyítás célja a téglalap területeinek egyenlőségének megállapítása A H J K (\displaystyle AHJK) négyzettel a láb fölött A C (\displaystyle AC); a második téglalap, amely a befogó feletti négyzet, és a másik láb feletti téglalap területeinek egyenlősége hasonló módon történik.
Egy téglalap területeinek egyenlősége A H J K (\displaystyle AHJK)és A C E D (\displaystyle ACED) háromszögek egybevágóságán keresztül állapítják meg △ A C K (\megjelenítési stílus \háromszög ACK)és △ A B D (\megjelenítési stílus \háromszög ABD), amelyek mindegyikének területe egyenlő a négyzetek területének felével A H J K (\displaystyle AHJK)és A C E D (\displaystyle ACED) rendre a következő tulajdonsággal kapcsolatban: a háromszög területe egyenlő a téglalap területének felével, ha az ábráknak közös oldaluk van, és a háromszög közös oldalának magassága a másik oldala a téglalap. A háromszögek egybevágósága a két oldal egyenlőségéből (a négyzetek oldalai) és a köztük lévő szögből (amely derékszögből és egy szögből áll A (\displaystyle A).
Így a bizonyíték azt állapítja meg, hogy a téglalapokból álló hipotenusz feletti négyzet területe A H J K (\displaystyle AHJK)és B H J I (\displaystyle BHJI), egyenlő a lábak feletti négyzetek területének összegével.
Leonardo da Vinci bizonyítéka
A területmódszer magában foglalja a Leonardo da Vinci által talált bizonyítást is. Legyen egy derékszögű háromszög △ A B C (\megjelenítési stílus \háromszög ABC) derékszög C (\displaystyle C)és négyzetek A C E D (\displaystyle ACED), B C F G (\displaystyle BCFG)és A B H J (\displaystyle ABHJ)(Lásd a képen). Ebben a bizonyításban az oldalon H J (\displaystyle HJ) az utóbbi, egy háromszög kifelé épül, egybevágó △ A B C (\megjelenítési stílus \háromszög ABC), ráadásul mind a hipotenuszhoz, mind a hozzá képesti magassághoz képest tükröződik (vagyis J I = B C (\displaystyle JI=BC)és H I = A C (\displaystyle HI=AC)). Egyenes C I (\displaystyle CI) a befogóra épített négyzetet két egyenlő részre osztja, hiszen háromszögek △ A B C (\megjelenítési stílus \háromszög ABC)és △ J H I (\megjelenítési stílus \háromszög JHI) felépítésében egyenlőek. A bizonyítás megállapítja a négyszögek egybevágóságát C A J I (\displaystyle CAJI)és D A B G (\displaystyle DABG), amelyek mindegyikének területe egyrészt egyenlő a lábakon lévő négyzetek területének felének, másrészt az eredeti háromszög területének összegével, másrészt a háromszög területének felével a hipotenuszon lévő négyzet plusz az eredeti háromszög területe. Összességében a lábak feletti négyzetek területének fele egyenlő a hipotenuzus feletti négyzet területének felével, ami megegyezik a Pitagorasz-tétel geometriai megfogalmazásával.
Bizonyítás infinitezimális módszerrel
A differenciálegyenletek technikájával számos bizonyítás létezik. Különösen Hardynak tulajdonítanak egy olyan bizonyítást, amely végtelenül kicsi lábnövekedést használ a (\displaystyle a)és b (\displaystyle b)és hypotenusa c (\displaystyle c), és az eredeti téglalappal való hasonlóság megőrzése, azaz a következő differenciális relációk teljesülésének biztosítása:
d a d c = c a (\displaystyle (\frac (da)(dc))=(\frac (c)(a))), d b d c = c b (\displaystyle (\frac (db)(dc))=(\frac (c)(b))).A változók szétválasztásának módszerével differenciálegyenletet vezetünk le belőlük c d c = a d a + b d b (\displaystyle c\ dc=a\,da+b\,db), amelynek integrálása adja a relációt c 2 = a 2 + b 2 + C o n s t (\displaystyle c^(2)=a^(2)+b^(2)+\mathrm (Const) ). A kezdeti feltételek alkalmazása a = b = c = 0 (\displaystyle a=b=c=0) egy állandót 0-ként definiál, ami a tétel állítását eredményezi.
A végső képletben a másodfokú függés a háromszög oldalai és a növekmény közötti lineáris arányosságból adódik, míg az összeg a különböző lábak növekményéből származó független hozzájárulásokból adódik.
Változatok és általánosítások
Hasonló geometriai formák három oldalon
A Pitagorasz-tétel fontos geometriai általánosítását adta Eukleidész a "Kezdetek"-ben, az oldalakon lévő négyzetek területeitől a tetszőleges hasonló geometriai alakzatok területei felé haladva: a lábakra épített ilyen alakzatok területének összege lesz megegyezik egy hozzájuk hasonló, a hipotenuszra épített figura területével.
Ennek az általánosításnak az a fő gondolata, hogy egy ilyen geometriai alakzat területe arányos bármely lineáris méretének négyzetével, és különösen bármely oldal hosszának négyzetével. Ezért hasonló számadatokhoz területekkel A (\displaystyle A), B (\megjelenítési stílus B)és C (\displaystyle C) hosszúságú lábakra épült a (\displaystyle a)és b (\displaystyle b)és hypotenusa c (\displaystyle c) ennek megfelelően van összefüggés:
A a 2 = B b 2 = C c 2 ⇒ A + B = a 2 c 2 C + b 2 c 2 C (\displaystyle (\frac (A)(a^(2)))=(\frac (B )(b^(2)))=(\frac (C)(c^(2)))\,\jobbra \,A+B=(\frac (a^(2))(c^(2) ))C+(\frac (b^(2))(c^(2)))C).Mivel a Pitagorasz-tétel szerint a 2 + b 2 = c 2 (\displaystyle a^(2)+b^(2)=c^(2)), akkor kész.
Ezen túlmenően, ha a Pitagorasz-tétel felhasználása nélkül be lehet bizonyítani, hogy egy derékszögű háromszög oldalain lévő három hasonló geometriai alakzat területére az összefüggés A + B = C (\megjelenítési stílus A+B=C), akkor az eukleidészi általánosítás bizonyításának fordítottját felhasználva levezethetjük a Pitagorasz-tétel bizonyítását. Például, ha a hipotenuszon egy derékszögű háromszöget készítünk, amely egybevágó a kezdeti területtel C (\displaystyle C), és a lábakon - két hasonló derékszögű háromszög területekkel A (\displaystyle A)és B (\megjelenítési stílus B), akkor kiderül, hogy a lábakon lévő háromszögek úgy keletkeznek, hogy a kezdeti háromszöget elosztjuk a magasságával, vagyis a háromszögek két kisebb területének összege megegyezik a harmadik területével, így A + B = C (\megjelenítési stílus A+B=C)és a relációt hasonló alakokra alkalmazva levezetjük a Pitagorasz-tételt.
Koszinusz tétel
A Pitagorasz-tétel egy speciális esete az általánosabb koszinusztételnek, amely egy tetszőleges háromszög oldalainak hosszát viszonyítja:
a 2 + b 2 − 2 a b cos θ = c 2 (\displaystyle a^(2)+b^(2)-2ab\cos (\theta )=c^(2)),hol van az oldalak közötti szög a (\displaystyle a)és b (\displaystyle b). Ha a szög 90°, akkor cos θ = 0 (\displaystyle \cos \theta =0), és a képlet a szokásos Pitagorasz-tételre egyszerűsödik.
Önkényes háromszög
Van a Pitagorasz-tétel általánosítása egy tetszőleges háromszögre, amely kizárólag az oldalak hosszának arányán működik, és úgy gondolják, hogy először Sabit ibn Kurra szabiai csillagász állapította meg. Ebben egy tetszőleges oldalú háromszöghez egy egyenlő szárú háromszög, amelynek oldala van c (\displaystyle c), a csúcs egybeesik az eredeti háromszög csúcsával, szemben az oldallal c (\displaystyle c)és az alapnál lévő szögek megegyeznek a szöggel θ (\displaystyle \theta ) ellenkező oldal c (\displaystyle c). Ennek eredményeként két háromszög keletkezik, hasonlóan az eredetihez: az elsőnek oldalai vannak a (\displaystyle a), a beírt egyenlő szárú háromszög tőle távol eső oldalsó oldala, és r (\displaystyle r)- oldalsó részek c (\displaystyle c); a második oldalról szimmetrikus rá b (\displaystyle b) bulival s (\displaystyle s)- az oldal megfelelő része c (\displaystyle c). Ennek eredményeként az összefüggés teljesül:
a 2 + b 2 = c (r + s) (\displaystyle a^(2)+b^(2)=c(r+s)),amely a Pitagorasz-tételig fajul at θ = π / 2 (\displaystyle \theta =\pi /2). Az arány a kialakult háromszögek hasonlóságának következménye:
c a = a r , c b = b s ⇒ c r + c s = a 2 + b 2 (\displaystyle (\frac (c)(a))=(\frac (a)(r)),\,(\frac (c) (b))=(\frac (b)(s))\,\Jobbra \,cr+cs=a^(2)+b^(2)).Pappus terület tétel
Nem euklideszi geometria
A Pitagorasz-tétel az euklideszi geometria axiómáiból származik, és a nem euklideszi geometriára érvénytelen – a Pitagorasz-tétel teljesülése egyenértékű az euklideszi párhuzamosság posztulátumával.
A nem euklideszi geometriában a derékszögű háromszög oldalai közötti kapcsolat szükségszerűen a Pitagorasz-tételtől eltérő formában lesz. Például a gömbgeometriában a derékszögű háromszög mindhárom oldala, amely az egységgömb oktánsát határolódik, hosszú π / 2 (\displaystyle \pi /2), ami ellentmond a Pitagorasz-tételnek.
Ráadásul a Pitagorasz-tétel érvényes a hiperbolikus és elliptikus geometriában, ha azt a követelményt, hogy a háromszög téglalap alakú, felváltjuk azzal a feltétellel, hogy a háromszög két szögének összege egyenlő legyen a harmadikkal.
gömbgeometria
Bármely derékszögű háromszögre egy sugarú gömbön R (\displaystyle R)(például ha a háromszögben a szög derékszögű) oldalakkal a , b , c (\displaystyle a,b,c) a felek közötti kapcsolat:
cos (c R) = cos (a R) ⋅ cos (b R) (\displaystyle \cos \left((\frac (c)(R))\right)=\cos \left((\frac) (a)(R))\jobbra)\cdot \cos \left((\frac (b)(R))\jobbra)).Ez az egyenlőség levezethető a gömb-koszinusz tétel speciális eseteként, amely minden gömbháromszögre érvényes:
cos (c R) = cos (a R) ⋅ cos (b R) + sin (a R) ⋅ sin (b R) ⋅ cos γ (\displaystyle \cos \left((\frac () c)(R))\right)=\cos \left((\frac (a)(R))\right)\cdot \cos \left((\frac (b)(R))\right)+\ sin \left((\frac (a)(R))\right)\cdot \sin \left((\frac (b)(R))\right)\cdot \cos \gamma ). ch c = ch a ⋅ ch b (\megjelenítési stílus \operátornév (ch) c=\operátornév (ch) a\cdot \operátornév (ch) b),ahol ch (\megjelenítési stílus \operátornév (ch) )- hiperbolikus koszinusz. Ez a képlet a hiperbolikus koszinusz tétel speciális esete, amely minden háromszögre érvényes:
ch c = ch a ⋅ ch b − sh a ⋅ sh b ⋅ cos γ (\megjelenítési stílus \operátornév (ch) c=\operátornév (ch) a\cdot \operátornév (ch) b-\operátornév (sh) a\cdot \operátornév (sh) b\cdot \cos \gamma ),ahol γ (\displaystyle \gamma )- olyan szög, amelynek csúcsa egy oldallal ellentétes c (\displaystyle c).
A Taylor sorozat használata a hiperbolikus koszinuszhoz ( ch x ≈ 1 + x 2 / 2 (\megjelenítési stílus \operátornév (ch) x\kb. 1+x^(2)/2)) kimutatható, hogy ha a hiperbolikus háromszög csökken (azaz mikor a (\displaystyle a), b (\displaystyle b)és c (\displaystyle c) nullára hajlamosak), akkor a derékszögű háromszög hiperbolikus relációi megközelítik a klasszikus Pitagorasz-tétel összefüggését.
Alkalmazás
Távolság kétdimenziós téglalap alakú rendszerekben
A Pitagorasz-tétel legfontosabb alkalmazása egy téglalap alakú koordinátarendszer két pontja közötti távolság meghatározása: távolság s (\displaystyle s) koordinátákkal ellátott pontok között (a , b) (\megjelenítési stílus (a,b))és (c , d) (\displaystyle (c,d)) egyenlő:
s = (a − c) 2 + (b − d) 2 (\displaystyle s=(\sqrt ((a-c)^(2)+(b-d)^(2)))).Komplex számok esetén a Pitagorasz-tétel természetes képletet ad a modulus komplex szám meghatározásához - z = x + y i (\displaystyle z=x+yi) hosszával egyenlő
Pitagorasz tétel- az euklideszi geometria egyik alaptétele, az összefüggés megállapítása
derékszögű háromszög oldalai között.
Úgy gondolják, hogy Pythagoras görög matematikus bizonyította be, akiről nevezték el.
A Pitagorasz-tétel geometriai megfogalmazása.
A tétel eredetileg a következőképpen fogalmazódott meg:
Egy derékszögű háromszögben a hipotenuszra épített négyzet területe egyenlő a négyzetek területének összegével,
katéterekre épített.
A Pitagorasz-tétel algebrai megfogalmazása.
Egy derékszögű háromszögben a befogó hosszának négyzete egyenlő a lábak hosszának négyzeteinek összegével.
Vagyis az átmenő háromszög befogójának hosszát jelöli c, és a lábak hossza át aés b:
Mindkét készítmény Pitagorasz-tételek egyenértékűek, de a második megfogalmazás elemibb, nem
terület fogalmát igényli. Vagyis a második állítás igazolható anélkül, hogy bármit is tudnánk a területről és
csak egy derékszögű háromszög oldalainak hosszát mérve.
Az inverz Pitagorasz-tétel.
Ha egy háromszög egyik oldalának négyzete egyenlő a másik két oldal négyzetösszegével, akkor
háromszög téglalap alakú.
Vagy más szóval:
A pozitív számok tetszőleges hármasára a, bés c, oly módon, hogy
van egy derékszögű háromszög lábakkal aés bés hypotenusa c.
Pitagorasz-tétel egyenlő szárú háromszögre.

Pitagorasz-tétel egyenlő oldalú háromszögre.

A Pitagorasz-tétel bizonyításai.
Jelenleg ennek a tételnek 367 bizonyítását rögzítették a tudományos irodalomban. Valószínűleg a tétel
Pitagorasz az egyetlen tétel, amely ilyen lenyűgöző számú bizonyítással rendelkezik. Ilyen sokszínűség
csak a tétel geometria szempontjából való alapvető jelentőségével magyarázható.
Természetesen fogalmilag mindegyik kis számú osztályra osztható. A leghíresebb közülük:
bizonyítéka terület módszere, magától értetődőés egzotikus bizonyíték(például,
használva differenciál egyenletek).
1. A Pitagorasz-tétel bizonyítása hasonló háromszögek szempontjából.
Az algebrai megfogalmazás következő bizonyítása a legegyszerűbb a megszerkesztett bizonyítások közül
közvetlenül az axiómákból. Különösen nem használja az ábra területének fogalmát.
Hadd ABC van egy derékszögű háromszög C. Rajzoljunk magasságot Cés jelöljük
az alapozását keresztül H.
Háromszög ACH háromszöghöz hasonló AB C két sarkon. Hasonlóképpen a háromszög CBH hasonló ABC.
A jelölés bevezetésével:

kapunk:
![]() ,
,
melyik egyezik -
Miután hajtogatta a 2 és b 2, kapjuk:
vagy , amit bizonyítani kellett.
2. A Pitagorasz-tétel bizonyítása területmódszerrel.
A következő bizonyítások látszólagos egyszerűségük ellenére egyáltalán nem ilyen egyszerűek. Mindegyikük
használja a terület tulajdonságait, amelyek bizonyítása bonyolultabb, mint magának a Pitagorasz-tételnek a bizonyítása.
- Bizonyítás egyenértékű kiegészítéssel.
 Rendezzünk el négy egyenlő téglalap alakút
Rendezzünk el négy egyenlő téglalap alakút
háromszög a képen látható módon
jobb oldalon.
Négyszög oldalakkal c- négyzet,
mivel két hegyesszög összege 90°, és
a kidolgozott szög 180°.
Az egész ábra területe egyrészt
egy négyzet területe oldalával ( a+b), másrészt pedig négy háromszög területének összege és
![]()
![]()
Q.E.D.
3. A Pitagorasz-tétel bizonyítása infinitezimális módszerrel.

Az ábrán látható rajzot figyelembe véve, ill
az oldalváltást figyelvea, tudunk
írd le a következő összefüggést a végtelenre!
kicsi oldalsó lépésekbenVal velés a(hasonlóságot használva
háromszögek):
A változók szétválasztásának módszerével azt találjuk, hogy:
Egy általánosabb kifejezés a hipotenusz megváltoztatására mindkét láb növekménye esetén:
Ezt az egyenletet integrálva és a kezdeti feltételek felhasználásával kapjuk:
Így elérkeztünk a kívánt válaszhoz:
Amint az jól látható, a végső képletben a másodfokú függés a lineárisnak köszönhető
arányosság a háromszög oldalai és a növekmény között, míg az összeg a függetlenhez viszonyít
a különböző lábak növekedéséből származó hozzájárulások.
Egyszerűbb bizonyítékot kaphatunk, ha feltételezzük, hogy az egyik láb nem tapasztal növekedést
(ebben az esetben a láb b). Ekkor az integrációs állandóhoz a következőket kapjuk: